形」と呼び,本研究では特徴的な双曲多角形の公式や性質について考えた.「対辺の長さ が等しい双曲4角形の性質」命題 33 や,「等辺直角 n 角形 ( 全ての辺の長さが等しく,全 多角形のうち、すべての辺の長さが等しいものは「正多角形」と呼ばれます。 正多角形の面積には公式があります。 正 (n) 角形の面積の公式公式を用意する V(体積) = 1/2 x 5 x 1辺の長さ x 辺心距離 x 角柱の高さとなります。 まず公式の前半部分で五角形の底面積を求めましょう。5つの三角形が合わさった多角形と考えましょう。

計算任意多邊形的面積 已知各頂點的坐標 碼上快樂
多角形 面積 公式 小学生
多角形 面積 公式 小学生- 多角形の内角の和と対角線の数の問題です。 公式を覚えておけば出来ますが、最近は公式の導き方を問うことも増えています。 丸暗記するのではなく、多角形の性質をしっかり確認して公式を使うようにしていきましょう。 多角形の内角の前回 https//wwwyoutubecom/watch?v=OfpWuAZA8uo&index=19&list=PLKRhhk0lEyzOfDE8u9U0GWX3aa43XeMOr 次回 https//wwwyoutubecom/watch?v=G4RJ4fV5k8&index
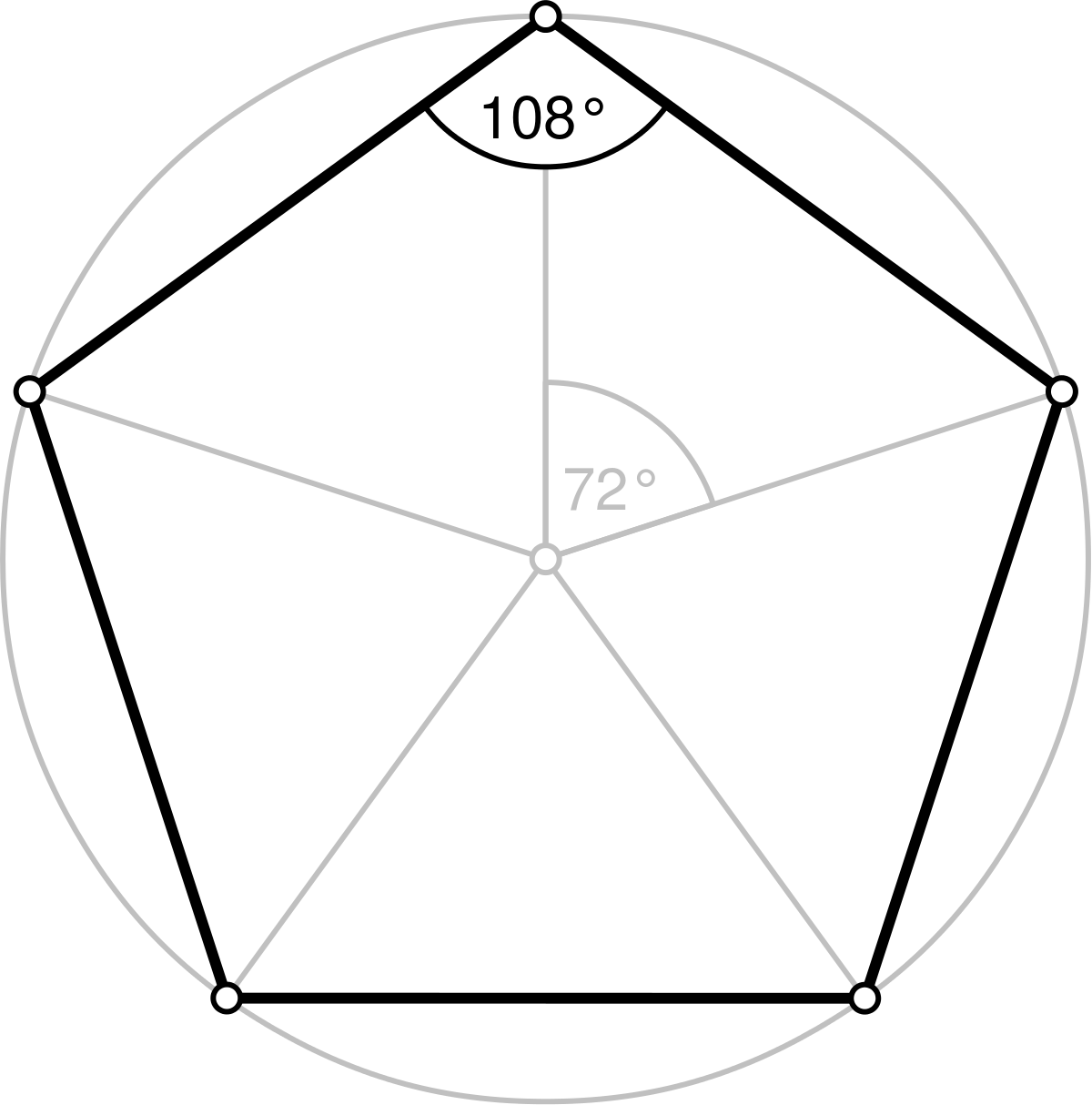



五边形 维基百科 自由的百科全书
球面上の多角形の面積と内角の和には美しい関係がある, というのが冒頭の定理です。三角形の場合が本質的です(証明は球面上の三角形の面積と内角の和を参照して下さい)。 三角形の場合を認めれば一般の n n n 角形については簡単に証明できます!概要 多角形の面積を計算する。 多角形の面積を求める公式が存在し、\(N\)個の点\(\mathbf{p_i} = (x_i, y_i)\)から成る多角形の面積\(S\)は以下の式で計算できる。台形の面積を求める公式は 台形の面積 上底 下底 高さ 台 形 の 面 積 = ( 上 底 下 底) × 高 さ ÷ 2 なので、 台形の面積 台 形 の 面 積 = ( 5 7) × 4 ÷ 2 = 12 × 4 ÷ 2 = 24 ( c m 2) になります。 次は小数点を含む台形の面積を計算します。
公式の導出方法 正多角形の面積導出には、sinで表す三角形の面積公式\(\frac{1}{2}\sin{\theta}ab\)を使用します この公式の導出についてはこちらの記事で解説していますので、興味のある方は是非ご覧ください sinで表す三角形の面積公式と導出方法 座標上の多角形の面積 #1 使えそうで使えない、だけどチョットだけ使えそうなオリジナル公式。 早稲田大学院生だったO君と開発したので、OK 定理とでも名付けましょうか。 座標上にある三角形P 1 P 2 P 3 の面積は、次のように求められる。 これはベクトルを利用した式で、高校入試の裏ワザ的な公式として紹介されているようです。 勘のいい人ならば、この式を2 ピックの公式 普通、多角形の面積を計算するときは、いくつかの三角形や四角形に分割 して、辺の長さなどを使って計算する。だが、ピックの公式は多角形上の格 子点の数を用いて面積を表す公式である。まずはピックの公式で扱う図形が
古典幾何における内接多角形の面積公式 早稲田大学大学院基幹理工学研究科数学応用数理学専攻 梅澤瑠奈(Runa UMEZAWA) 1 はじめに ユークリッド幾何では三角形のときHeron の公式, 内接四角形のときBrahmagupta の公式など、面積をその辺 ひし形(対角線直交四角形)の面積=対角線×対角線÷2 円周=直径×円周率(314)=半径×2×円周率(314) 円の面積=半径×半径×円周率(314) おうぎ形の弧の長さ=円周×中心角/360=直径×314×中心角/360ピックの定理(ていり、Pick's theorem)は等間隔に点が存在する平面上にある多角形の面積を求める公式である。 この場合の多角形の頂点は全て右図のように格子点(等間隔に配置されている点)上にあり、内部に穴は開いていないものとする。 多角形の内部にある格子点の個数を i、辺上に



等腰三角形面积公式 等腰三角形面积公式 尚书坊




八角形计算公式 八角形有哪些计算公式 三人行教育网 Www 3rxing Org
Title 円内接多角形問題について 半径公式と面積公式の統合 (数式処理とその周辺分野の研究) Author(s) 森継, 修一正 n n 角形の面積 1辺の長さが a a である正 n n 角形の面積 Sn S n は、次の公式で求められる Sn = na2 4tan π n S n = n a 2 4 tan 正多角形の面積 1辺の長さが a a である正多角形の面積は、次の公式で求められる 正三角形 = √3 4 a2 正四角形 =a2 正五角形 = √2510√5 4 a2 正六角形 = 3√3 2 a2 正 三 角 形 = 3 4 a 2三角形の面積を求める公式 三角形の面積を求める公式といえば「底辺×高さ÷2」を思い出しますが、ここでは「サインを使って三角形の面積を求める公式」を紹介します。 図のような abcの面積をsとしたとき 公式の証明 ではこの公式を証明してい




等边直三角形面积公式 西瓜视频




用三角形面積公式 揭開了鮮為人知的小秘密 顛覆了學數學的認識 每日頭條
以上のことから,半径公式と面積公式を ' 統合した公式" は, $Z=z^{2}=(4SR)^{2}$ (ただし, $S$多角形の 面積 $R$外接円半径) とおくと, $n=3,$$n=4$ のそれぞれに対して, $za_{1}a_{2}a_{3}=0$ および $Za_{1}^{2}a_{2}^{2}a_{3}^{2}=0\backslash$ (10)三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから)任意多角形の面積および頂点列の回転方向 31 任意多角形の面積の公式および回転方向の判定方法 32 3次元空間内の任意多角形の面積 4 任意多角形の断面1次モーメントおよび重心 (図心) 41 任意多角形の断面1次モーメントの公式 (Y/X軸まわり) 42 任意多角形の重心 (図心) の公式 5




八边形 维基百科 自由的百科全书
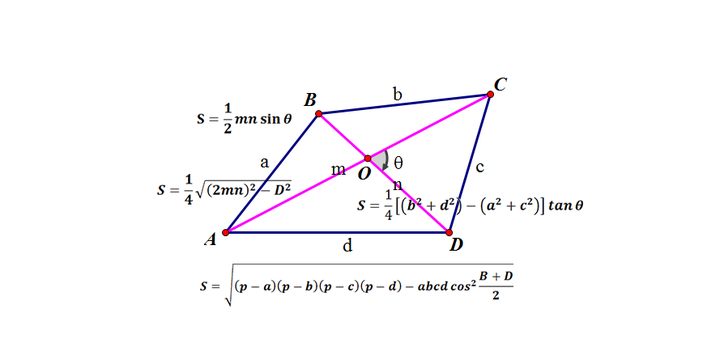



四边形的面积公式 知乎
多角形の面積を求める公式を導け. 耳(対角線によって切り取ることが できる三角形)の存在を仮定して 証明せよ. レポート課題1(1) 耳の存在を仮定して, 公式を証明せよ.面積計算の研究 ご意見・ご感想 任意の座標点で囲まれる三角形の面積と周囲の長さを計算します。となっていますが,三角形は多角形では? keisanより ご指摘ありがとうございます。 修正しました。 面積公式 多角形の面積は、頂点の位置ベクトルから 外積 を用いて計算することができる。 多角形の頂点を反時計回りに並べて、それらの位置ベクトルを p → 1 , , p → n {\displaystyle {\vec {p}}_ {1},\dots , {\vec {p}}_ {n}} とすると、その面積は 1 2 ∑ k = 1 n p → k × p → k 1 {\displaystyle {\frac {1} {2}}\sum _ {k=1}^ {n} {\vec {p}}_ {k}\times {\vec {p}}_ {k1}} という式になる




拋物線中動態幾何圖形面積問題 一 Itw01



锐角三角形的计算公式 3角形面积计算公式 尚书坊
三角形の面積の公式 三角形の一辺の長さを『底辺』とし、頂点から底辺に向かって垂直に下ろした線の長さを『高さ』と言います。 このとき三角形の面積は『底辺×高さ ÷2 ÷ 2 』で求めることができます。 例題を見てみましょう。 例題 底辺 6cm 6 c m円に内接する四角形 $\mathrm {ABCD}$ において, $a = \mathrm {AB},$ $b = \mathrm {BC},$ $c = \mathrm {CD},$ $d = \mathrm {DA},$ $s = \dfrac {abcd} {2}$ とおく このとき, 四角形の面積5 定理の公式と上記の格子多角形の面積を求める計算例 S = m + n / 2 S:格子多角形の面積 m:完全な枠(格子1マス)の数(下図のピンクの枠) n:不完全な枠(1本の辺と格子枠に囲まれている枠)の数(下図のグリーンの枠)




解析一道經典小學數學多邊形面積計算題 組合圖形面積計算 好題 雪花新闻




高校数学 正十二角形の周長と面積 多角形の求積の原則 受験の月
面積の求め方の基本(たて×よこ) 小学生の算数で習う多角形の 面積の公式で一番の基本 は タテ×ヨコ です。 小学生が習う算数では、多角形の面積の公式は タテ×ヨコ に戻せます。 では、どうやったら タテ×ヨコ に戻せるのか? これを理解する事で公式の成り立ち(公式が考えられた理この講習では、平面上の多角形であって、x 座標、y 座標がともに整数である多角形(格子多角 形) の面積を中心に解説します。格子多角形の面積公式としては、ピックの定理が有名ですが、加 えて、類似の定理である、森原の定理や額賀の定理も紹介します。 4つの面積の公式をおさらいしておきましょう。★三角形底辺×高さ÷2 ★平行四辺形平行四辺形だけは÷2しない!底辺×高さ ★台形(上底+下底)×高さ÷2 ★ひ




利用行列式計算多邊形面積 線代啟示錄




計算任意多邊形的面積 已知各頂點的坐標 碼上快樂
多角形 面積 座標 公式1辺の長さを \(~a~\) とした、正多角形の面積を一般化した形で求めます。 Ⅰ 面積の公式(一般化) Ⅱ 例 Ⅲ 面積の公式(一般化)の証明 Ⅳ 円の面積へ Ⅰ 面積の公式 以前の記事で、正任意多角形の断面m次モーメント 21 三角形の面積公式の証明 冒頭に述べた球面三角形の面積公式 s = r 2 (a b c − π) s=r^2(abc\pi) s = r 2 (a b c − π) を証明します。 まず二つの大円のなす角が a a a である状況を考えます。二つの大円によって球面は4つに分割されます。多角形の内部にある格子点の個数を i 、 辺 上にある格子点の個数を b とするとこの種の多角形の面積 S は以下の式で求められる。 例えば図の六角形なら内部にある点が i = 39 個、辺上にある点が b = 14 個なので S = 39 14/2 − 1 = 45 と簡単に計算できる。



四边形的面积公式 知乎




面積 32 求三角形的 高 的進階練習 Youtube
円内接多角形問題について —半径公式再論* 森継修一 shuichi moritsugut 筑波大学図書館情報メディア系 faculty of library, information and media science, university of tsukuba 1 はじめに 円内接多角形問題とは, 「円に内接する n 角形の各辺の長さ a_{1}, a2, , a_{n} が与えられた 1辺の長さが a a である正多角形の面積は、次の公式で求められる。 正三角形 = √3 4 a2 正四角形 = a2 正五角形 = √2510√5 4 a2 正六角形 = 3√3 2 a2 正 三 角 形 = 3 4 a 2 正 四 角 形 = a 2 正 五 角 形 = 25 10 5 4 a 2 正 六 角 形 = 3 3 2 a 2 4種類挙げましたが、正四角形(正方形)は当然知っているはずですし、正五角形は使用頻度が少ないうえに複雑すぎて覚えるのは 1 辺の長さが分かっている時は公式を用いる 基本の六角形は6つの二等辺三角形で構成されているので、その公式もまた二等辺三角形の面積を求める公式が元になっています。 六角形の面積(A)を求める公式は A = (3√3 s2)/ 2 となり、 s が辺の長さを指しています。 {"smallUrl""https\/\/wwwwikihowcom\/images_en\/thumb\/e\/eb\/CalculatetheAreaofa




平行四邊形面積計算公式




計算任意多邊形的面積 已知各頂點的坐標 碼上快樂
Wikipediaに多角形の面積の公式も載っていた。 外積ってなんだったっけ?(汗) 内積はなんとなく覚えてるけど。 まあ、ようするに、上の三角形の面積を全部足し合わせるってことだよな。 三角形とポリゴンの面積は、こちらの説明もわかりやすかった。実は、一般的に次の公式により、機 械的な計算で面積は求められる。 n 個の頂点の座標を、(X k ,Y k )とす ると、面積Sは、 但し、X n+1 =X 1 ,Y n+1 =Y 1 試しに、上記の図形の面積を求めてみよここでは、プログラムでよく使われる。数学の公式・定理を紹介します。 例えば、三角形の5心(重心、内心、傍心、外心、垂心)、多角形の面積・重心計算などです。 重心:3つの中線の交点 内心:3つの角の2等分線の交点 傍心:1つの頂点における内角の2等分線と,他の2つの頂点における外角




多边形的面积 天明天明 博客园



周长 面积 体积 玄数
多角形の面積計算機(ヘロンの公式利用) 多角形を三角形で分割し、それぞれの面積をヘロンの公式で計算し、元の多角形の面積を求積します。 ぱっと見て理解できる人用です。 細かい説明はしません。 まあ普通はエクセルとかでやることです。 計算結果表をCSVファイル(エクセル等で扱えます)でダウンロードできます。 行(三角形)の数 5 / 10 / / 30 / 50



1




面積計算公式gmath Pripdw




五年級上數學多邊形面積的應用題 壹讀




角形余弦公式 搜索结果 哔哩哔哩 Bilibili




正多边形面积 内角和 外接圆 内切圆在线计算器 三贝计算网 23bei Com



矩形面積公式epistemath 數學知識 Wjklv



坡度面积计算公式图解 信息阅读欣赏 信息村 K0w0m Com




平行四邊形面積公式



长方形面积计算公式长方形平方面积公式怎么算 Python编程长方形面积公式




海龍公式 維基百科 自由的百科全書




多边形面积 Segmentfault 思否




五边形 维基百科 自由的百科全书



正多角形の面積の公式 一般化 Fukusukeの数学めも
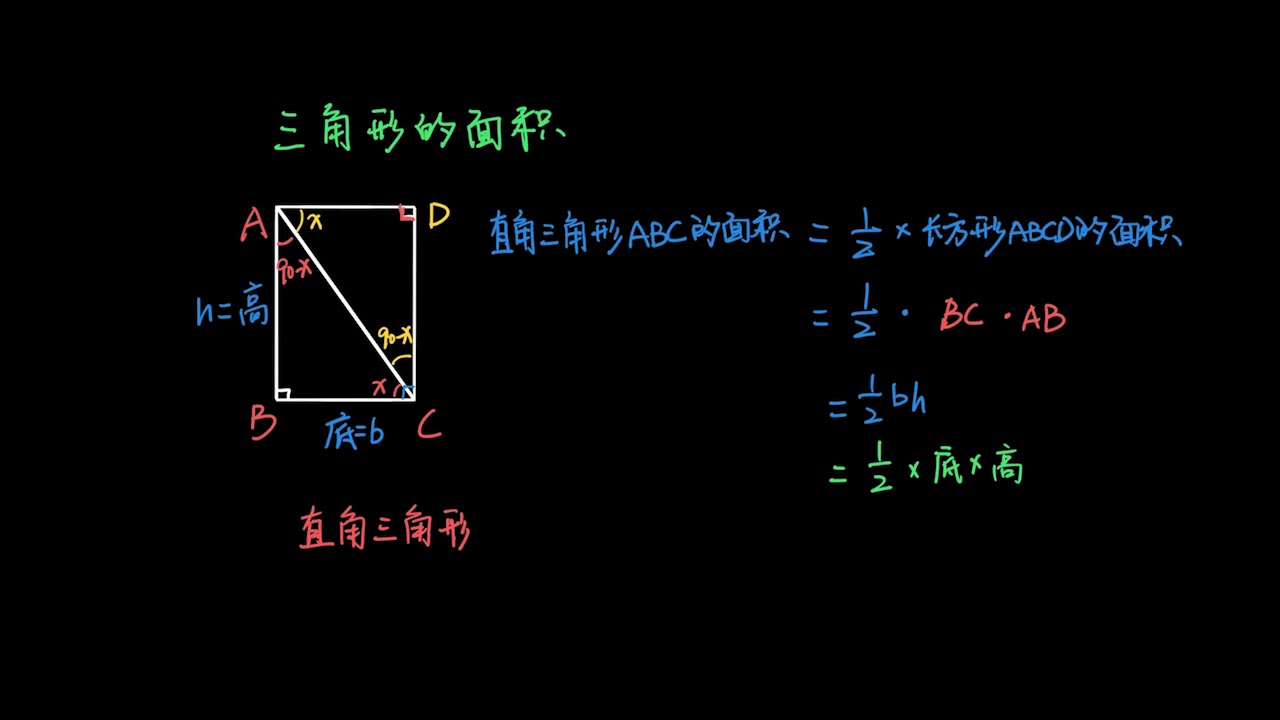



五年级数学41 多边形的面积 三角形面积公式证明 Youtube
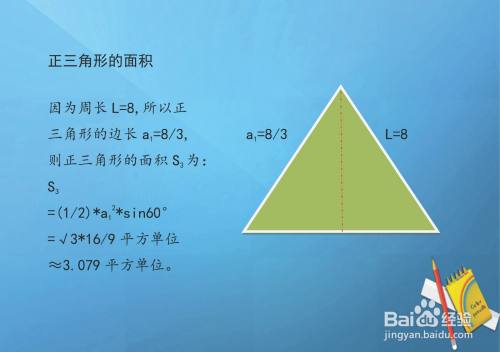



已知周长l 8 求正三角形等多边形和圆的面积 百度经验
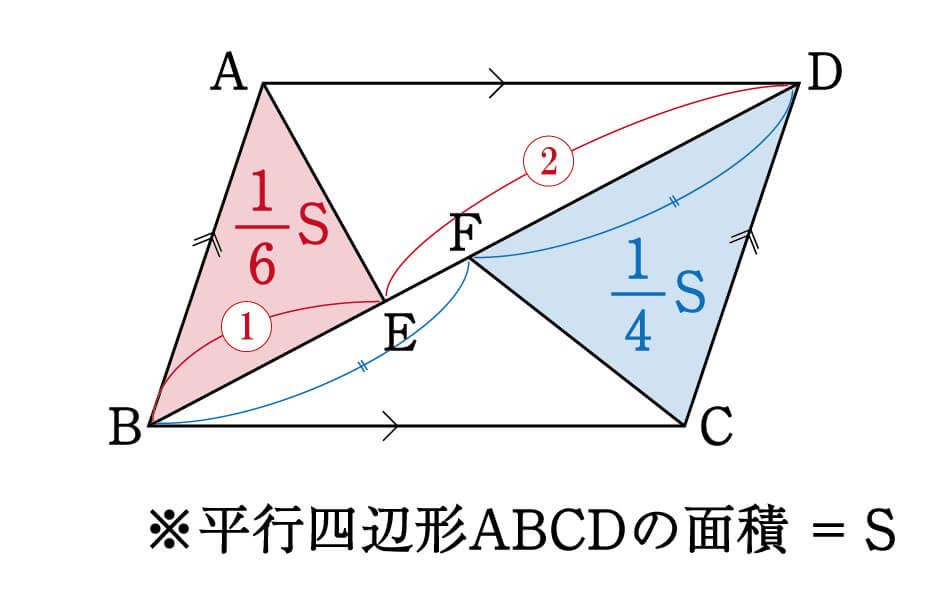



平行四邊形面積公式




常用圖形求面積計算公式 人人焦點
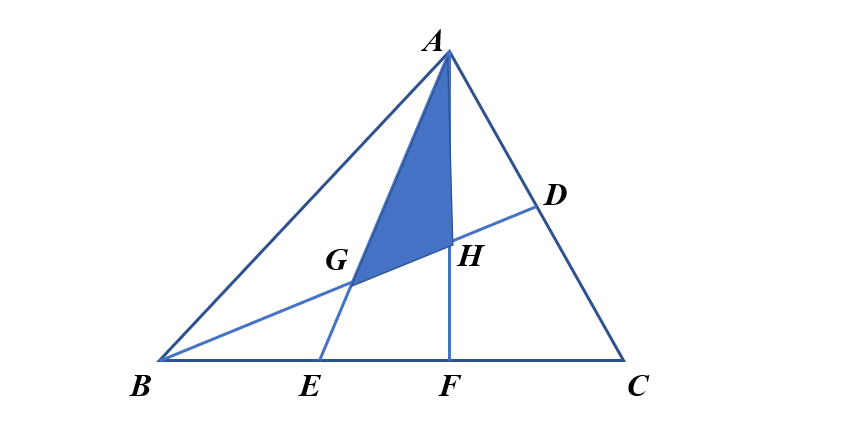



C 三角形的面积 Csdn



课堂实录 圆的面积 六上 雪花新闻




三角函數六角形正多角形の面積 Pbhcl




Pk Ckcos6 正多邊形面積公式



1




小五多邊形面積練習19 Lvai



三角形面积计算公式 三角形面积公式 越多越好 100查分网




扇形面积公式 搜索结果 哔哩哔哩 Bilibili



高中数学 纯干货 三角形的30个面积公式总结 高中生快来收 初中




正投影公式祖暅原理與正投影面積公式 Mrsysy



平行四邊形面積公式



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



2




数学趣谈 球面积公式的不同导出方法 参考网




六边形面积怎么算 百度经验




高能預警 多邊形面積如何計算 小心被虐哭 一 每日頭條




平面上任意多邊形求面積的方法 Youtube



三角形面积计算公式 三角形面积公式 越多越好 100查分网




一般 正三角形的高與面積 Youtube
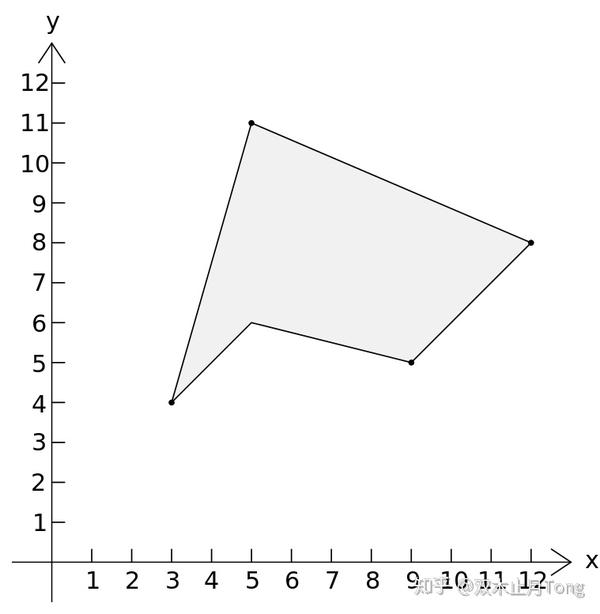



国际数学竞赛 任意多边形面积计算公式 知乎
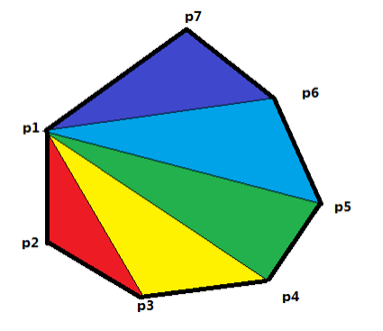



多边形的面积 天明天明 博客园



1




固定边长多边形的面积问题 Sqr5 S Blog



锐角三角形的计算公式 3角形面积计算公式 尚书坊



最高のコレクション多角形面積公式 犬イラスト




正多角形の面積 倭算数理研究所




Pk Ckcos6 正多邊形面積公式




五年級數學月考必備 多邊形的面積計算單元重點 老師嘔心總結 每日頭條




求任意多邊形面積 台部落




怎么求六边形面积 生活百科




如何计算多边形面积 15 步骤




多邊形面積 1 Youtube




梯形面積計算方法平行四邊形 三角形和梯形的面積 Wjklv
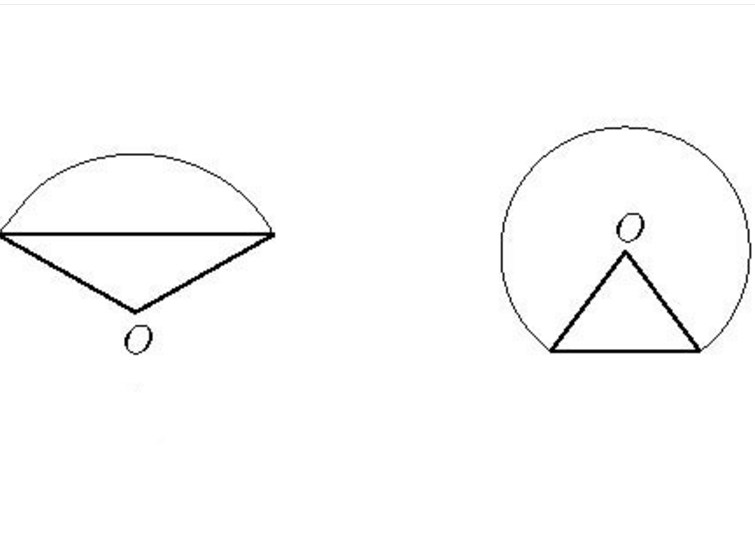



弓形面積公式 基本介紹 廣義弓形面積公式 中文百科全書



平行四邊形面積公式




如何计算多边形面积 15 步骤



几何 玄数 Page 3



快收藏 建築工程施工 裝修常用的各種圖形計算公式都在這了 雪花新闻




数学趣谈 球面积公式的不同导出方法 参考网
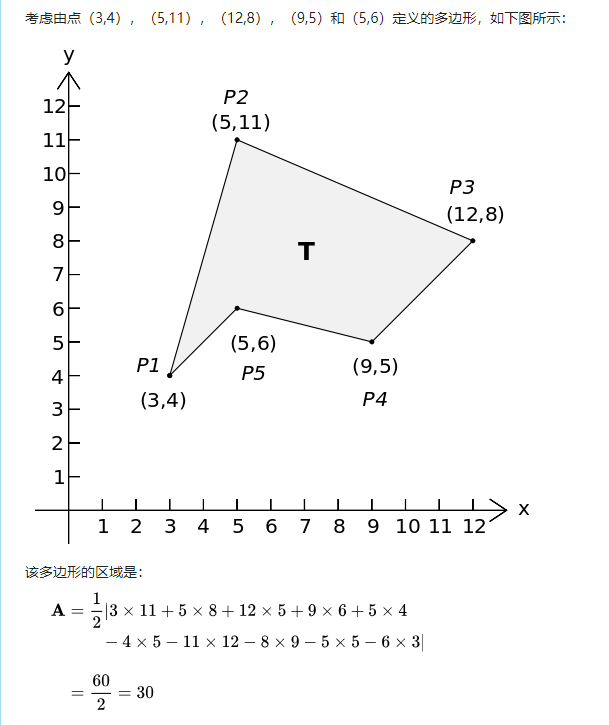



C 多边形面积计算公式 Khandasas 博客园




最も欲しかった 多角形面積公式 ユニークな壁紙サイトhd




正三角形面積公式證明從三角形的面積談起 Mrsysy




三角形正多边形面积公式 三角形png图片素材免费下载 图片编号 Png素材网



四边形的面积公式 知乎



利用行列式計算多邊形面積 線代啟示錄



三角形面积计算公式 三角形面积公式 越多越好 100查分网
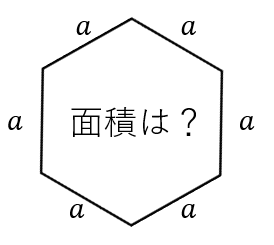



正六角形の面積 計算ツール 公式の導出 具体例で学ぶ数学
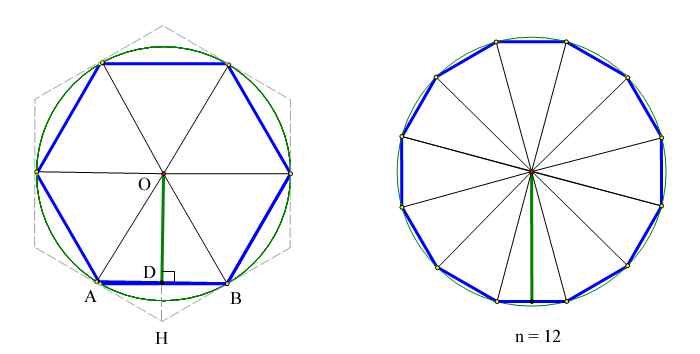



正多邊形的一些基本概念 知乎




如何求正多边形的面积 7 步骤




任意多邊形的面積計算 台部落




小三 周長與面積 求正多邊形周長 重點講解 Youtube




梯形面積對角線三角形 平行四邊形 梯形 多邊形面積公式怎麼記 親子天下 Qavhp



利用行列式計算多邊形面積 線代啟示錄



六邊形面積公式六邊形 Kdnbe



改革春风吹满地 多边形面积的求法 用到矩阵 Dsh0106的专栏 Csdn博客




正三角形面積公式證明從三角形的面積談起 Mrsysy




平行四邊形的面積公式




4种方法来求六边形面积



高中数学 纯干货 三角形的30个面积公式总结 高中生快来收 初中



1




八角形畫法sketchup Uhlwc




最新のhd五角形面積公式



平行四邊形面積公式




如何求正多边形的面积 7 步骤




如何求正多边形的面积 7 步骤



利用行列式計算多邊形面積 線代啟示錄




直角锥体积 表面积 侧面积 计重 报价计算公式与在线计算器 三贝计算网 23bei Com
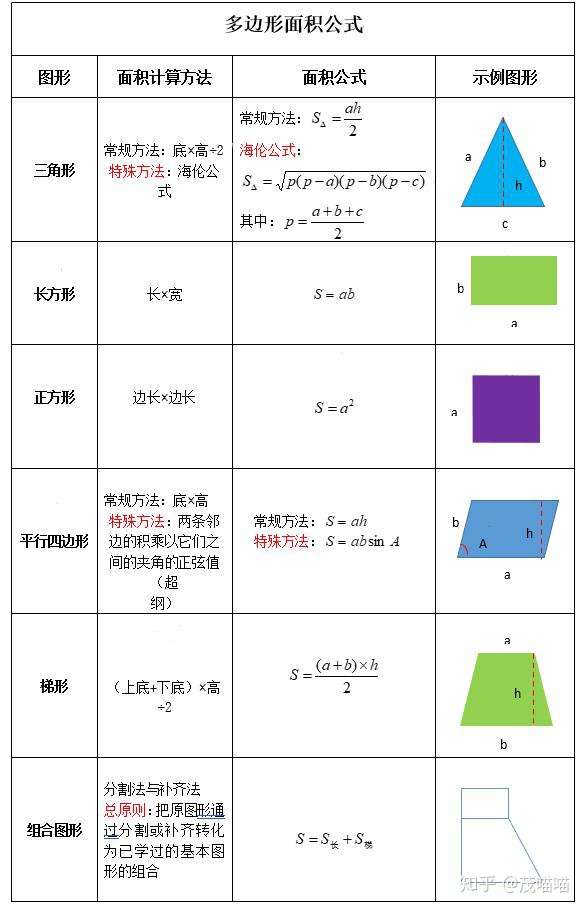



五年级数学知识点总结 04多边形面积 知乎




如何求正多边形的面积 7 步骤



0 件のコメント:
コメントを投稿